The post contains my writeup to SCYPHER - Substitution Cipher SPOJ problem.

1. Problem description

Full problem statement is provided here.

In short, we have a number of lexicographically sorted texts, that were encrypted with bijective substitution cipher. Texts are followed a secret message encrypted with the same substitution cipher. The task is to determine if it is possible to decrypt the message and, if it is possible, to decrypt it.

I will refer to i’th letter of k’th decrypted text as \(a_{k,i}\) and to i’th letter of k’th encrypted text as \(b_{k,i}\).
\(a_{k,i} < a_{l,j}\) for characters \(a_{k,i}\) and \(a_{l,j}\) if \(a_{k,i}\) is earlier in the alphabet than \(a_{l,j}\).
\(b_{k,i} < b_{l,j}\) for characters \(b_{k,i}\) and \(b_{l,j}\) if \(a_{k,i} < a_{l,j}\).
\(f\) will denote substitution function i.e. \(f(a_{k,i})=b_{k,i}\). Let \(s_i\) be \(f(\)i’th letter of alphabet\()\) i.e. \(s_1=f(a)\), \(s_3=f(c)\) etc. \(s_i < s_j\) if \(i < j\).
\(A\) will denote size of substitution cipher.

2. Observations

1. \(b_{k,i} = b_{m,j} \implies a_{k,i} = a_{m,j}\) and \(b_{k,i} \neq b_{m,j} \implies a_{k,i} \neq a_{m,j}\).
   Explanation: This follows directly from bijection property of substitution cipher.

2. If \(b_{k,m} = b_{k+1,m}\) for all \(m < n\) and \(b_{k,n} \neq b_{k+1,n}\), then \(a_{k,n} < a_{k+1,n}\).
   Explanation: Because \(b_{k,m} = b_{k+1,m}\) for \(m < n\) it follows from the first observation that \(a_{k,m} = a_{k+1,m}\) for \(m < n\) and because \(b_{k,n} \neq b_{k+1,n}\) it follows that \(a_{k,n} \neq a_{k+1,n}\). Not encrypted texts are sorted lexicographically, so if \(a_{k,m} = a_{k+1,m}\) for \(m < n\) and \(a_{k,n} \neq a_{k+1,n}\), then \(a_{k,n} < a_{k+1,n}\). It also means that \(b_{k,n} < b_{k+1,n}\).

3. If we found \(<\) relation between all different values \(b_{k,m}\), \(b_{l,n}\), we could recover substitution cipher.
   Explanation: If we found \(<\) relation between all different values \(b_{k,m}\), \(b_{l,n}\), we could create a chain \(b_1 < b_2 < ... < b_A\), where \(b_{i}=b_{l,m}\) for some l,m. It is easy to show that if \(b_{k,i} = s_m\) and \(b_{l,j} = s_n\), then \(b_{k,i} < b_{l,j}\) if and only if \(s_m < s_n\). So chain \(b_1 < b_2 < ... < b_K\) is equivalent to chain \(s_{i_1} < s_{i_2} < ... < s_{i_A}\) where \(s_{i_k}=b_k\). Because the chain contains all values of \(f\) and \(s_i < s_j\) if \(i < j\) it follows that \(s_{i_k}=s_k\). This way we recovered substitution function mapping.

3. Solution

Lets collect all pairs \(b_{k,n}\), \(b_{k+1,n}\) for which \(b_{k,m} = b_{k+1,m}\) for \(m < n\) and \(b_{k,n} \neq b_{k+1,n}\). Lets create a directed graph with nodes being character values of encrypted texts - size of this graph is of course \(A\). Two nodes u and v are connected with edge directed from u to v if there is pair \(b_{k,n}=u\), \(b_{k+1,n}=v\) such that \(b_{k,n} < b_{k+1,n}\). It is easy to show that the graph is acyclic. For any path \(P=p_1, p_2, ... , p_n\) the property \(p_i < p_j \iff i < j\) holds (every \(p_i\) is some \(b_{j,n}\)). From these statements it follows that path going exactly once through all vertices of the graph would form the sequence \(s_1, ... , s_K\). Such path can be computed by topological sort algorithm - ordering returned by the algorithm is the path. From the path a reverse substitution cipher mapping \(f^{-1}\) can be calculated as \(f^{-1}(p_i)=i\) where \(p_i\) is the i’th vertex in the path and i is the i’th letter of the alphabet. The secret message can be decrypted by applying \(f^{-1}\) to its letters. One quirk from the problem statement: if a letter in encrypted message does not belong to substitution alphabet, then the letter is not encrypted and should be left unmodified in decrypted message.

If a path passing through all vertices does not exist in the graph, there are some vertices between which there is no path - if there was a path between every two vertices all vertices could be ordered by \(<\) relation and path going through all vertices could be computed. In this case the program returns “Message cannot be decrypted.”. However for some cases this is not be true (message can be decrypted), which will be discussed in the next section.

Full implementation written in Rust is available here.

3.1 Example

Lets demonstrate how my solution works for input data from problem statement:

5 6
cebdbac
cac
ecd
dca 
aba   
bac   
cedab   

Alphabet size is 5.
Following is the list of lexicographically sorted and then encrypted texts: cebdbac, cac, ecd, dca, aba, bac.
From the list we can derive the following pairs \(b_{k,n}\), \(b_{k+1,n}\) for which \(b_{k,m} = b_{k+1,m}\) for \(m < n\) and \(b_{k,n} < b_{k+1,n}\):
\(e < a\) (texts 1 and 2, second position)
\(c < e\) (texts 2 and 3, first position)
\(e < d\) (texts 3 and 4, first position)
\(d < a\) (texts 4 and 5, first position)
\(a < b\) (texts 5 and 6, first position)

Based on these pairs we create a graph:

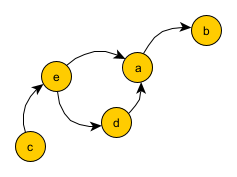
Topological sort applied to the graph returned the following ordering: c, e, d, a, b. Reverse substitution cipher mapping \(f^{-1}\) looks like this:
\(f^{-1}(c) = a\)
\(f^{-1}(e) = b\)
\(f^{-1}(d) = c\)
\(f^{-1}(a) = d\)
\(f^{-1}(b) = e\)

Applying the function to letters of the encrypted secret message ‘cedab’ will return ‘abcde’.

4. Not fully recovered substitution cipher may be sufficient

In the previous section I wrote that if there is no path going through all vertices, my code returns “Message cannot be decrypted.” My solution was accepted by SPOJ checker, but there are some cases where knowing whole path is not necessary to decrypt secret message.

Lets go through a testcase posted in the problem comments.

4 6
a
bc
bd
bdc
bdb
d
bd

From the list of encrypted text we can derive the following pairs \(b_{k,n}\), \(b_{k+1,n}\) for which \(b_{k,m} = b_{k+1,m}\) for \(m < n\) and \(b_{k,n} < b_{k+1,n}\):
\(a < b\) (texts 1 and 2, first position)
\(c < d\) (texts 2 and 3, second position)
\(c < b\) (texts 4 and 5, third position)
\(b < d\) (texts 5 and 6, first position)

Based on these pairs we create a graph:

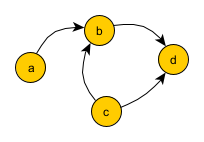
Topological sort applied to the graph returns either a, c, b, d or c, a, b, d. It is not possible to determine whether \(a<c\) or \(c<a\). However encrypted message does not contain letters a and c, only b and d. In any topological sort ordering b and d will be the last two letters of the path. Therefore \(f^{-1}\) for b and d looks like this:
\(f^{-1}(b) = c\)
\(f^{-1}(d) = d\)
So ‘bd’ can be unambiguously decrypted to ‘cd’ for any topological sort. However, if the secret message was ‘ad’ it would not be possible to decrypt the message.

If for every alphabet letter in secret message we can compute \(f^{-1}\) the message can be decrypted. \(f^{-1}\) can be calculated for a vertex if its position among other vertices can be determined unambiguously. The question is: How to check if position of a vertex in ordering returned from topological sort is the only possible one?

Thesis:
Position of a vertex v in topological sort ordering is the only possible one, if and only if for every u other than v there is a path from u to v or from v to u.
Proof:
Consider a vertex v in DAG.
If for every u other than v there is a path from u to v or from v to u, then in any topological sorting ordering there will always be the constant number of vertices before v (elements from which there is path to v) and constant number of vertices after v (elements to which there is path from v).

On the other hand: lets assume that there is some vertex which is not connected with v. I will construct another ordering where position of v is changed.
Lets take any topological ordering and let u be the vertex which is not connected with v and which is closest (in terms of positions difference) to v in the ordering. Lets consider all possible positions of u and v in the ordering:
Case 1: u and v are next to each other
Swapping u with v will form another valid topological sort, where position of v is changed.
Case 2: There are vertices between u and v, u is before v in the ordering
Total ordering contains the following fragment: \(u,x_1,x_2,...,x_n,v\). Because u is the closest vertex to v which is not connected to v the following relation holds: relation \(x_1 < v, x_2 < v, ..., x_n < v\). u cannot be connected to any of \(x_1,x_2,...,x_n\), because there would be path from u to v. In that case replacing \(u,x_1,x_2,...x_n,v\) in the total ordering with \(x_1,x_2,...,x_n,v,u\) will form a valid ordering, where position of v is changed.
Case 3: There are vertices between u and v, u is after v in the ordering
This is symmetrical to the previous case. Fragment \(v,x_1,x_2,...,x_n,u\) can be replaced with \(u,v,x_1,x_2,...,x_n\)
Q.E.D.

Using above thesis we can check for every vertex v in polynomial time (e.g. with DFS on original DAG and DAG with inversed edges) if there are paths connecting all other vertices with v.

Lets apply this approach to the example from the beginning of this section: There is no path between a and c. Other letters are connected with all letters in the graph. So \(f^{-1$}\) can be determined only for b and d (\(f^{-1}(b) = c\), \(f^{-1}(d) = d\)).

5. Is this solution always correct?

Unfortunately I have no proof that there is no smarter algorithm which would decrypt test cases, for which my solution would return “Message cannot be decrypted.”.